
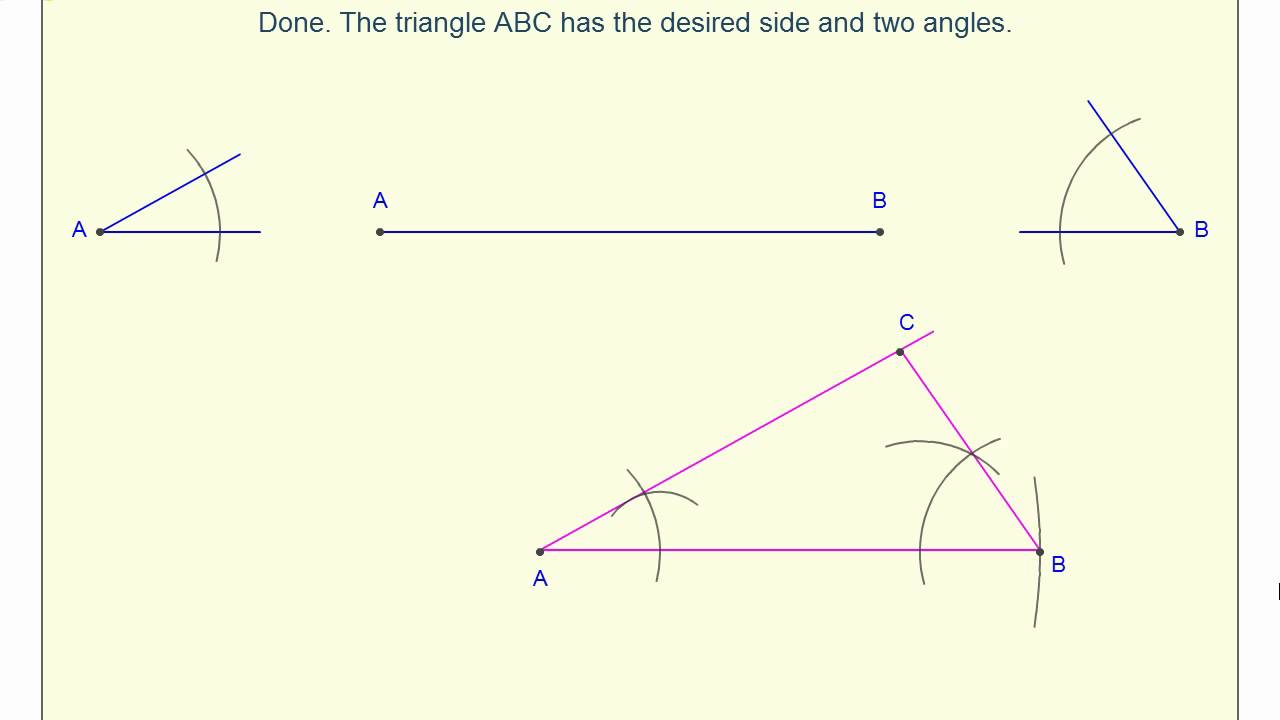
This is the first of many theoremsabout isosceles triangles. These are the angles opposite the congruent sides in ABC. For example, if ABC is an isosceles triangle with ¯AB ~= ¯BC, you can show that ABC ~= CBA by SAS.
Most of these will be proven using the SAS postulate. You will see several theorems about isosceles triangles. The side-angle-side theorem is one of three theorems for showing that two triangles are congruent the other two are the angle-side-angle (ASA) theorem and the. As long as you are careful to discuss two sides and the included angle, you'll be fine. The sides that include these angles are ¯MN and ¯PN (for QNP). Notice that the angles you are focusing on are MNP and QNP. Use the rflexive property of ~= to obtain another set of congruent sides: A side is congruent to itself. The congruence of one set of sides is given. Because ¯PN ¯MQ, you know that right angles are formed. SAS AAS ASA HL Use tick marks and arcs to indicate the remaining corresponding congruent parts.
EXPLAINING SAS GEOMETRY HOW TO
MMonitoring Progressonitoring Progress Help in English and Spanish at Explain how to show that the indicated triangles are similar. Yes, you can make the right end similar to the left end of the shelter. Explain Sallys reasoning for why triangle ABC is congruent to triangle DEF using the language of reflections: Construct a reflection which maps point A to. Solution: The game plan is to make use of the SAS Postulate. So, by the SAS Similarity Theorem, ABC FGH.Therefore, the distance between the airplanes is approximately $1982.6$ km after three hours. Determine the measure of the third angle by subtracting the already measured angles (given angle and the angle determined in step 2) from $180^$.Use the Law of Sines to find the angle (acute angle) opposite the smaller of the two sides.Use the Law of Cosines to measure the missing side.Sometimes we do not know the measures of.
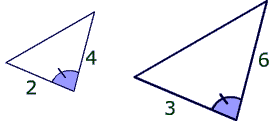
When we know the measure of two sides and the included angle, we can apply a three-step method to solve a SAS triangle: using the Law of Cosines, using the Law of Sines, and determining the measure of the third angle. SSS tells us that if all the corresponding sides of the triangle are of equal length, then the triangles are congruent. The reason for a strange, asymmetric formulation is that Elements I.4 is about what is known nowadays as SAS and establishes the congruence of two triangles by. Listed below are a few topics related to the SSA congruence rule, take a look. Therefore, it is proved that the SSA congruence rule is not valid. In other words, congruence through SAS is valid. Figure 14-1 illustrates a triangular combination which is known as a SAS triangle. A pair of sides and the included angle will uniquely determine a triangle. We can observe that we are given two sides $b$ and $c$, and the included angle $\alpha$. Decide whether the triangles are congruent, explaining your reasoning. SAS (side-angle-side) triangle is basically a triangular combination when we know the measure of two sides of a triangle and the angle between them.Ĭonsider a triangle $△ABC$ with the sides $a$, $b$, and $c$ facing the angles $\alpha$, $\beta$, and $\gamma$, respectively, as shown in Figure 15-1.


 0 kommentar(er)
0 kommentar(er)
